Introducción
Como ya se ha comentado antes, todos los sonidos generados por la naturaleza, inclusive los generados por la vibración de cualquier elemento como puede ser una cuerda de una guitarra, o el aire que pasa dentro de los tubos de un instrumento de viento, además de la frecuencia principal que generan, producen armónicos, generalmente con volumen mas bajo, y guardan una relación matemática con el sonido principal, esta relación es el doble de la frecuencia del sonido principal, el triple, cuatro veces la frecuencia del sonido principal, etc..
Es esta la razón por la cual el oído humano, junto con el cerebro, han evolucionado de forma tal, que al escuchar los sonidos cuyas frecuencias están en la proporción simple (2/1, 3/2, 4/3,etc.), los reconoce como un sonido agradable.
La variedad de tonos que nuestro oído es capaz de percibir es muy elevada, estando acotada tan sólo por los límites de sensibilidad de nuestro sistema auditivo, normalmente desde los 20hz hasta los 20.000hz. Teniendo en cuenta que el oído humano puede diferenciar sonidos con 1hz de diferencia, bien podríamos tener una cantidad ingente de notas en nuestra escala musical. Ahora bien, de este espectro sonoro es preciso elegir ciertas frecuencias o tonos con las que podamos disponer de un conjunto de sonidos que permitan la construcción de las melodías. Del mismo modo que un pintor requiere unos determinados colores en su paleta para hacer sus cuadros, el músico necesita una escala musical concreta con la que componer y ejecutar su música.
La gama usual de frecuencias de los sonidos musicales, es considerablemente más pequeña que la gama audible, siendo el tono más alto de un piano el de frecuencia 13.186 Hz, este valor podemos considerarlo como el límite superior de los tonos fundamentales.
En esta sección únicamente se pretenden plasmar los conceptos musicales básicos que posibiliten la futura comprensión de los términos empleados en el estudio de los instrumentos musicales. Si usted está interesado en profundizar o ampliar éstos, y otros conceptos usados en música, puede acceder a los siguientes enlaces.
El origen de la escala musical
En música, al emitirse dos o más sonidos simultáneos, se dice que se produce un "acorde", que puede ser "consonante" o "disonante", según que la sensación experimentada sea agradable o desagradable, cuando la sensación agradable es producida por una sucesión de sonidos, entonces se tiene una "melodía". La experiencia enseña que la sensación producida no depende de los valores absolutos de las frecuencias de los sonidos, sino de la relación entre ellas, es decir, del intervalo (cociente de las frecuencias, tomando siempre como numerador la mayor frecuencia), siendo esta sensación tanto más agradable, cuanto más sencillo sea el intervalo entre los dos sonidos.
Como vemos, la melodía consiste en la elección y número de notas que componen un período musical, por ejemplo en las obras de tipo orquestal, la melodía es interpretada por el solista, siendo acompañado por el resto de la orquesta que proporciona la armonía.
El lenguaje empleado en música contiene una serie de expresiones cuyo significado físico interesa conocer, como por ejemplo: a) tesitura (tono de un sonido); b) color (características propias del timbre); c) crescendo ydescrecendo (intensidad de un sonido que aumenta o disminuye); d) fuerte, piano, pianísimo (máxima intensidad que puede producirse, sonido suave y muy suave); el trémolo (producir una nota de frecuencia fundamental inferior a los 16 Hz, aunque rica en armónicos); f) vibrato (variaciones rápidas y pequeñas en el tono de una nota).
La escala actual (escala occidental) es el resultado de un largo proceso de aprendizaje de las notas. Los pitagóricos construyeron un aparato llamado monocordio que se componía de una tabla, una cuerda tensa y una tabla más pequeña que se iba moviendo por la grande.
|  |
 |
Monocordio
|
Los pitagóricos observaron que haciendo más o menos larga la cuerda (moviendo la tabla móvil) se producían sonidos diferentes. Entre estos sonidos escogieron algunos que eran armoniosos con el sonido original (cuerda entera).
La figura representa a Pitágoras estudiando las relaciones entre la tensión de las cuerdas y el sonido para una longitud igual de las mismas. Se trata de un grabado del libro "Theorica Musicae", de Franchino Gaffurio (Biblioteca Trivulziana-Milán).
En la música es muy importante la relación que existe entre la frecuencia de los distintos sonidos, a esta relación se le llama intervalo. Los intervalos musicales pueden medirse en términos de la relación de frecuencias de los sonidos, aunque en música reciben nombres propios cuya correspondencia física depende del tipo de escala utilizada.
Los más importantes, por su simplicidad y su importancia a la hora de construir la escala musical, son:
- La octava. Cuando la cuerda medía un medio del total, el sonido se repetía, pero más agudo. La octava es lo que correspondería a un salto de ocho teclas blancas del piano; o mejor dicho, una octava es la repetición de un sonido con una cuerda con la mitad de longitud, por tanto, otra nota armoniosa. Su frecuencia es doble.
- La quinta es otro intervalo entre notas que se obtiene con una cuerda de largura dos tercios de la inicial. Su frecuencia es de tres medios del sonido inicial. Corresponde a un salto de cinco teclas blancas en un piano.
- La cuarta es, como las anteriores, otro intervalo entre notas que se obtiene con una cuerda de largura tres cuartos de la inicial. Su frecuencia es cuatro tercios de la nota inicial.
As�, a partir de un sonido original obtenemos diferentes notas armoniosas. Haciendo un peque�o esquema nos aclararemos mejor:
Nota
|
Frecuencia
|
Long. cuerda
|
Original
|
F
|
L
|
Octava justa
|
2f
|
1/2�L
|
Quinta mayor
|
3/2�f
|
2/3�L
|
Cuarta justa
|
4/3�f
|
3/4�L
|
| Tercera mayor | 5/4�f | 4/5�f |
| Tercera menor | 6/5�f | 5/6�f |
Si suponemos que la nota inicial es el do, entonces, la octava, quinta y cuarta son las notas:
Nota base
|
Cuarta
|
Quinta
|
Octava
|
Do
|
Fa
|
Sol
|
Do (1 octava más alta)
|
Que corresponden a la cuarta, quinta y octava notas respectivamente de la escala diatónica (las teclas blancas del piano), que veremos un poco más adelante.
Se puede definir un etalón como una nota estándar de la cual podemos derivar todas las otras notas. Para entender como es la relación entre las notas musicales y como se definieron estas a través de los años, vamos a establecer una primera nota fundamental o estándar que será la nota de La central que tiene una frecuencia de 440 Hz. Aquí podemos ver dos dibujos con un fragmento de las teclas del piano con el nombre que reproduce su nota musical, además se encuentra la frecuencia que produce esa nota musical.
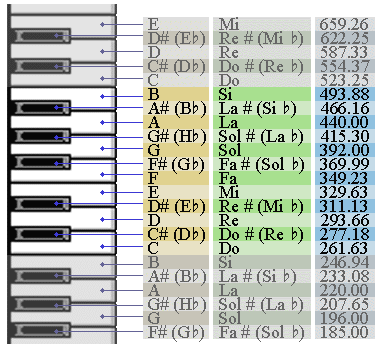
En estos esquemas se puede ver que las teclas forman grupos de 12 (7 blancas y 5 negras), y estos grupos se repiten de izquierda a derecha. Cada ocho teclas blancas se cierra un grupo y se abre otro, y la distancia musical entre esas teclas se llama octava (normalmente se llama octava también el mismo grupo de 12 teclas), y su escala es igual a 2:1 - esto es, la frecuencia de la misma nota de siguiente octava es el doble, y la de octava anterior es la mitad. La distancia de dos octavas le corresponde a la relación de frecuencias de 4:1, tres octavas - 8:1 etc.: para sumar distancias tenemos que multiplicar las relaciones de frecuencias. La nota "La" (o "A") es la nota de etalón - su frecuencia es 440 Hz.
Esta ordenación de los sonidos musicales ha sido fruto de un largo proceso. Desde la elección de un sonido base, a partir del cual construir el resto, a la determinación del intervalo que hay entre una nota y la siguiente.
Así, una escala es una serie de notas ordenadas de forma ascendente o descendente, donde a la primera de las notas se la llama tónica.
El nombre de las notas musicales
El italiano Guido de Arezzo, (995-1050), en plena Edad Media, - en el año 1026 -introdujo el pentagrama e inventó la escritura de las notas, (do, re, mi, fa, sol, la). Arezzo, para crear su escala musical, utilizó la primera sílaba de cada verso de un himno dedicado a San Juan, que se atribuye a Paulo Diácono y que decía:
Ut queant laxis
Resonare libris Mira gestorum Famuli tuorum Solve polluti Labii reatum Sancte Joannes |  |
Más tarde, por las dificultades para cantar, la ut se cambió por do. Pero debieron transcurrir cinco siglos, hasta el XVI, para que se completara la escala musical, tal como hoy la conocemos. Se recurrió al mismo himno que Arezzo había utilizado en el siglo XI, y con las iniciales de San Juan que, por entonces, se escribía Sante Ioanes, y se formó la séptima nota - SI - y la octava fue la repetición del Do.
Actualmente también se utilizan las letras A, B, C, D, E, F, G para designar las notas musicales.
Las denominaciones más comunes de los sonidos son
| Inglés: | C D E F G A B |
| Alemán: | C D E F G A H |
| Español, italiano y francés: | Do Re Mi Fa Sol La Si |
Estas son las 7 notas de la escala diatónica. De cualquier forma, en una octava se utilizan 12 notas (las de la escala cromática). Las 5 notas restantes se simbolizan añadiendo a la derecha el carácter # (sostenido) o b (bemol).
En música la representación gráfica de los sonidos se hace por medio de unos símbolos (las notas), que se escriben sobre una pauta llamada pentagrama. El pentagrama es una manera de realizar una notación musical de tal modo que la misma sea fácilmente transmisible a otras personas. Esto significa que así como las letras del alfabeto se juntan para formar una frase, de la misma manera los símbolos musicales se juntan en el pentagrama para formar una canción que puede ser interpretada por un instrumento musical o cantada por la voz del ser humano.
Un típico pentagrama en clave de Sol
Básicamente los pentagramas están formados por un conjunto de cinco líneas dispuestas de forma paralela. A la izquierda del conjunto de líneas aparece un símbolo distintivo llamado "clave". Esta clave es la que determinará a qué nota musical corresponde cada uno de los símbolos musicales que aparecen en el pentagrama. En el gráfico anterior encontramos un símbolo que identifica a la "clave de Sol":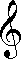 
. Existe una variedad considerable de claves en otras notas como Do y Fa , por ejemplo. Como vemos a continuación, el símbolo de la clave de Fa es: 
. Existe una variedad considerable de claves en otras notas como Do y Fa , por ejemplo. Como vemos a continuación, el símbolo de la clave de Fa es: 
Un pentagrama en clave de Fa
Las notas musicales que aparecen dentro del pentagrama pueden colocarse justo encima de alguna de las líneas o en los espacios entre las mismas. Según la clave que corresponda (Sol, Do, Fa, etc.) y la ubicación específica entre las líneas, cada símbolo musical nos brindará información sobre una única nota. La duración en el tiempo de la misma vendrá dada por las características del símbolo musical utilizado.
La nota, gracias a su aspecto y su posición, permite definir simultáneamente tres parámetros:
- La posición vertical de la nota define su altura (aguda o grave). Cuanto más arriba se sitúe la nota sobre las líneas o los espacios del pentagrama, más aguda será.
- La posición horizontal de la nota define cuando es emitida. Así, el eje horizontal del pentagrama define una escala de tiempo creciente desde la izquierda hacia la derecha. Si existiesen dos notas en la misma columna, estarían emitidas simultáneamente.
- La forma de la nota define su duración. Duraciones estándar de notas están definidas en solfeo; cada una es dos veces más corta que la siguiente. Así, se tiene:
La redonda
, blanca 
, negra 
, corchea 
, semicorchea 
, fusa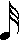 
, etc.
La redonda
, blanca , negra , corchea , semicorchea , fusa , etc.
Así, una blanca es dos veces más corta que una redonda, una negra dos veces más corta que una blanca...
Tomando como base la frecuencia 55Hz (que en la escala musical es el LA más grave del piano) y a esta frecuencia la multiplicamos por 2, luego por 3 y así sucesivamente, obtendremos distintas frecuencias, que además constituyen distintas notas musicales. A estas frecuencias las colocaremos en una tabla y asignaremos su equivalente nota musical.
1� Octava
|
55
| |||||||
2� Octava
|
110
|
165
| ||||||
3� Octava
|
220
|
275
|
330
|
385
| ||||
4� Octava
|
440
|
495
|
550
|
605
|
660
|
715
|
770
|
825
|
5� Octava
|
880
| |||||||
| La | Si | Do | Re | Mi | Fa | Sol | ||
A
|
B
|
C
|
D
|
E
|
F
|
G
|
H
|
Observamos que la primera octava tiene sólo una nota que tiene la frecuencia 55hz, la segunda octava tiene dos notas con las frecuencias 110hz y 165hz, la tercera octava cuatro notas con las frecuencias 220hz, 275hz, 330hz y 385hz, y la cuarta octava tiene ocho frecuencias, o sea, ocho notas. Estamos frente a una octava completa natural. Ahora vamos a calcular las distancias entre las notas:
440
|
8:9
|
495
|
9:10
|
550
|
10:11
|
605
|
11:12
|
660
|
12:13
|
715
|
13:14
|
770
|
14:15
|
825
|
15:16
|
880
|
A4
|
B4
|
C5
|
D5
|
E5
|
F5
|
G5
|
H5
|
A5
| ||||||||
1:1
|
9:8
|
5:4
|
11:8
|
3:2
|
13:8
|
7:4
|
15:8
|
2:1
|
En las celdas superiores intermedias se indica la distancia entre las frecuencias vecinas, y en las celdas inferiores, la distancia con respecto a la frecuencia principal, que en nuestro ejemplo es 440 Hz. La numeración de octavas (4� o 5�) corresponde al estándar contemporáneo.
El producto de todas las relaciones intermedias es igual a 2, esto es, a una octava. La escala que acabamos de construir se conoce como escala natural.
La distancia musical entre la nota principal (La 55 Hz) y la segunda armónica (La 110 Hz) es 2/1(octava).
La distancia musical entre la segunda armónica (La 110 Hz) y la tercera armónica (Mi 165 Hz) es 3/2 (quinta), como entre las notas A4 y E5
La distancia entre la tercera armónica (Mi 165 Hz) y la cuarta armónica (La 220 Hz) es de 4/3 (cuarta), como entre las notas E5 y A5.
La Escala Pentatónica
Los músicos antiguos, que no tenían el concepto de escala natural, intuitivamente ajustaban (afinaban) las cuerdas (o en el caso de instrumentos de viento, adecuaban su longitud y grosor, distancia entre agujeros, etc.) de manera que produjeran un sonido lo más agradable posible para el oído humano.
Dentro de una octava, la combinación de sonidos más pura es la quinta, es decir, el intervalo musical entre dos notas cuyas frecuencias se relacionan como 3:2. (En nuestro ejemplo, estas notas son A y E) Al escoger como la base la nota A4, iremos dos quintas arriba y abajo, tenemos la siguiente serie de 5 sonidos: 195.5556, 293.3333, 440, 660, 990
Estas frecuencias están más cerca de las notas: G3, D4, A4, E5 y B5. Vamos a transportarlas a la misma octava (multiplicando o dividiendo por 2 cuando sea necesario) y calcular las distancias entre las notas:
293.33
|
8:9
|
330.00
|
27:32
|
391.11
|
8:9
|
440.00
|
8:9
|
495.00
|
27:32
|
586.67
|
D4
|
E4
|
G4
|
A4
|
B4
|
D5
|
La distancia de 9/8 se llama tono (T). La distancia de 32/27 es igual a 1.5 tonos (TS). Esta serie de cinco intervalos musicales, T-TS-T-T-TS se llama escala pentatónica, y el sistema musical en que se usa esta escala, se llamapentafonía.
La pentafonía se usa en la mayoría de los sistemas musicales tradicionales, ya que es la escala más simple e intuitiva. Este es un ejemplo - un fragmento de un tema andino (escuchar
):
):
Cabe mencionar que se puede escoger como base cualquiera de las 12 notas del piano y construir una escala pentatónica. Por ejemplo, las cinco teclas negras forman precisamente una pentafonía.
Se sabe que los Egipcios ya conocían y aplicaban la escala pentatónica. El famoso mural en el palacio de Asshurbanipal's representa la orquesta de la corte Elamita. En este mural se puede observar que están tocando una armonía simple basada en las quintas (Curt Sachs, The Rise of Music in the Ancient World: East and West, first edition [W.W. Norton, 1943]).
La Escala Diatónica
Ya sabemos que dos notas de una quinta producen juntas un sonido agradable. Dentro de la quinta, se encuentra un sonido más formando un triplete en que las frecuencias se relacionan como 4:5:6. Este triplete se llama armonía. La escala natural tiene una sola combinación armónica, las notas A-C-E. Al descubrir la armonía, los músicos antiguos empezaron a afinar sus instrumentos de manera que toda la escala musical fue compuesta de armonías continuas, como esta:
352
|
4:5
|
440
|
5:6
|
528
|
4:5
|
660
|
5:6
|
792
|
4:5
|
990
|
5:6
|
1188
|
F4
|
A4
|
C5
|
E5
|
G5
|
B5
|
D6
|
Vamos a construir una octava y calcular la distancia entre las notas vecinas:
264
|
8:9
|
297
|
9:10
|
330
|
15:16
|
352
|
8:9
|
396
|
9:10
|
440
|
8:9
|
495
|
15:16
|
528
|
C4
|
D4
|
E4
|
F4
|
G4
|
A4
|
B4
|
C5
| |||||||
do
|
re
|
mi
|
fa
|
sol
|
la
|
si
|
do
|
Esta serie de notas o distancias entre ellas se llama escala diatónica. La distancia de 9/8 es un tono, la distancia de 10/9 está muy cerca y se llama tono menor, y la distancia de 16/15 es aproximadamente igual a una mitad del tono, y se llama semitono. La serie de tonos (T) y semitonos (S): T-T-S-T-T-T-S, donde el semitono es el tercer intervalo, se llama tonalidad mayor. Para construir una tonalidad menor tenemos que iniciar esta secuencia desde la nota A: T-S-T-T-S-T-T. Aquí el semitono es el segundo. La diferencia entre estas tonalidades ya había sido descubierta por los músicos antiguos: la misma melodía tocada en tonalidades diferentes (mayor o menor), tiene un carácter diferente, lo que permite expresar sentimientos mediante la variación de la tonalidad de la música. Las canciones que usan una tonalidad mayor son alegres y vivaces, mientras que las que usan una tonalidad menor son tristes y melancólicas.
Como un ejemplo ilustrativo, podemos escuchar este fragmento de una balada folklórica rusa «No es de noche» en la tonalidad de «Sol menor» (Gm) (escuchar):
):
La misma melodía tocada en la tonalidad de «Do mayor» (C) tiene un carácter mucho más alegre y optimista (escuchar):
):
Otra vez, podemos escoger como base para construir una tonalidad, cualquiera de las 12 notas, 24 diferentes en total. Estas tonalidades llevan el nombre de la nota principal y la palabra "mayor" o "menor", por ejemplo, «Do mayor» o C, «La menor» o Am, etc.
A continuación indicamos las distancias de las notas en una tonalidad mayor respeto a la nota principal y sus nombres:
264
|
297
|
330
|
352
|
396
|
440
|
495
|
528
|
C4
|
D4
|
E4
|
F4
|
G4
|
A4
|
B4
|
C5
|
1
|
9:8
|
5:4
|
4:3
|
3:2
|
5:3
|
15:8
|
2
|
primera
|
segunda
|
tercera
|
cuarta
|
quinta
|
sexta
|
séptima
|
octava
|
La Escala Cromática o Temperada
Al descubrir las tonalidades, los músicos antiguos quisieron tener la posibilidad de pasar libremente entre ellas. Evidentemente, para hacerlo, se necesitan construir escalas mayores y menores comenzando con cada una de las siete notas que tenemos. Los resultados de esos cálculos están presentados en la siguiente tabla:
A
|
275.00
|
293.33
|
330.00
|
366.67
|
412.50
|
440.00
|
495.00
| |||||
Am
|
264.00
|
297.00
|
330.00
|
352.00
|
396.00
|
440.00
|
495.00
| |||||
B
|
278.44
|
309.38
|
330.00
|
371.25
|
412.50
|
464.06
|
495.00
| |||||
Bm
|
278.44
|
297.00
|
334.13
|
371.25
|
396.00
|
445.50
|
495.00
| |||||
C
|
264.00
|
297.00
|
330.00
|
352.00
|
396.00
|
440.00
|
495.00
| |||||
Cm
|
264.00
|
297.00
|
316.80
|
356.40
|
396.00
|
422.40
|
475.20
| |||||
D
|
278.44
|
297.00
|
334.13
|
371.25
|
396.00
|
445.50
|
495.00
| |||||
Dm
|
267.30
|
297.00
|
334.13
|
356.40
|
400.95
|
445.50
|
475.20
| |||||
E
|
275.00
|
309.38
|
330.00
|
371.25
|
412.50
|
440.00
|
495.00
| |||||
Em
|
264.00
|
297.00
|
330.00
|
371.25
|
396.00
|
445.50
|
495.00
| |||||
F
|
264.00
|
293.33
|
330.00
|
352.00
|
396.00
|
440.00
|
469.33
| |||||
Fm
|
264.00
|
281.60
|
316.80
|
352.00
|
396.00
|
422.40
|
475.20
| |||||
G
|
264.00
|
297.00
|
330.00
|
371.25
|
396.00
|
445.50
|
495.00
| |||||
Gm
|
267.30
|
297.00
|
316.80
|
356.40
|
396.00
|
445.50
|
475.20
| |||||
C
|
D
|
E
|
F
|
G
|
A
|
B
|
Esta tabla tiene 25 sonidos diferentes (18 nuevos). Y esto no es todo, porque cada uno de esos nuevos sonidos puede engendrar su propia escala, tanto mayor como menor - ¡la octava al final va a tener cerca de 100 notas! Sería sumamente difícil tocar un instrumento de tantas teclas. Los griegos antiguos hicieron un compromiso: introducir notas "extra" sólo donde el intervalo entre las notas vecinas sea un tono entero (C-D, D-E, F-G, G-A, A-B), de manera que la distancia mínima dentro de una octava sea igual a un semitono. Como resultado de esto, las notas adicionales obtenidas ocupan las posiciones donde se encuentran las teclas negras del piano.
Pitágoras propuso derivar todas las 12 notas de puras quintas (de la misma manera que nosotros lo hicimos para construir una escala pentatónica). Vamos a empezar otra vez con la nota A4 que tiene la frecuencia de 440Hz, pasar quinta a quinta 6 veces arriba, sucesivamente multiplicando la frecuencia por 3/2, y 6 quintas abajo, dividiendo por 3/2:
38.63
|
57.94
|
86.91
|
130.37
|
195.56
|
293.33
|
440.00
|
660.00
|
990.00
|
1485.00
|
2227.50
|
3341.25
|
5011.88
|
D#1
|
A#1
|
F2
|
C3
|
G3
|
D4
|
A4
|
E5
|
B5
|
F#6
|
C#7
|
G#7
|
D#8
|
La primera y la última nota de esa escala es la misma nota D#, aunque de diferentes octavas, la D#8 está a siete octavas arriba del # . Aquí surge un problema: en esta escala no es posible pasar directamente de D#1 a D#8 octava a octava (multiplicando por 2 la frecuencia). Las 7 octavas no son iguales a las 12 quintas. Esta discrepancia (que es igual a (3/2)12 : 27 = 1.013643 aproximadamente, o sea, 0.2346 de semitono) lleva el nombre de coma pitagoreana. Si queremos preservar pura la quinta, tenemos que cambiar la octava, que es una distancia aún más fundamental en la música.
La última reforma musical fue inspirada por un organista alemán, Andreas Werckmeister, a fines del siglo XVII. él propuso hacer todos los semitonos iguales. El problema planteado así tiene una única solución: la distancia musical entre cada una de las notas vecinas debe ser igual a la raíz doceava de 2, o sea, 21/12. Este sistema por lo general se denomina sintonización bien temperada o temperamento igual. La escala de 12 semitonos iguales se llamaescala cromática. Cada semitono a su vez se divide en 100 partes iguales que se llaman centavos de semitono. El temperamento asimismo altera la quinta, que llega a ser un poco más corta, y modifica también las demás distancias naturales, quedando pura únicamente la octava. Las ventajas obtenidas son evidentes: ahora se puede pasar libremente entre tonalidades, y de esta manera, se logró eliminar la coma pitagoreana.
Finalmente vamos a comparar la escala natural, la escala pitagoreana y la escala cromática:
Natural
|
275.00
|
302.50
|
330.00
|
357.50
|
385.00
|
412.50
|
440.00
|
495.00
| ||||
Pitagoreana
|
260.74
|
278.44
|
293.33
|
309.03
|
330.00
|
347.65
|
371.25
|
391.11
|
417.66
|
440.00
|
463.54
|
495.00
|
Cromática
|
261.63
|
277.18
|
293.66
|
311.13
|
329.63
|
349.23
|
369.99
|
392.00
|
415.30
|
440.00
|
466.16
|
493.88
|
C
|
C#
|
D
|
D#
|
E
|
F
|
F#
|
G
|
G#
|
A
|
A#
|
B
|
Para calcular la frecuencia de cada nota en la escala cromática, dada su escala (a cuantas teclas está de la nota de etalón La), se usa la siguiente fórmula: Fi = 440 * 2i/12
Aquí i es la escala o la distancia de la nota de etalón. Si es negativa, la tecla está a la izquierda.
Ejemplo: la frecuencia de la nota Do (que está 9 teclas a la izquierda) es: 440 * 2-9/12 = 261.63
